티스토리 뷰
강한 결합 요소란 그래프 안에서 '강하게 결합된 정점 집합'을 의미한다. 서로 긴밀하게 연결되어 있다고 하여 강한 결합 요소라고 말한다.
SCC는 '같은 SCC에 속하는 두 정점은 서로 도달이 가능하다'라는 특징이 있다.
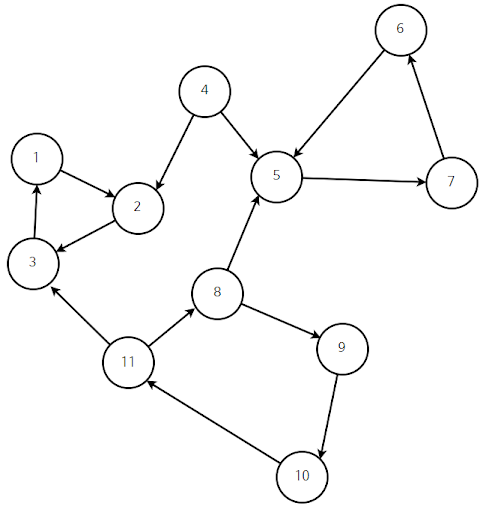
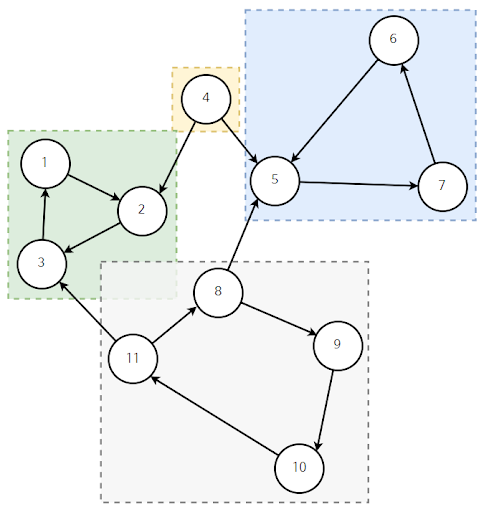
총 4개의 집합이 존재하는데 각 집합에 있는 정점끼리는 서로에게 도달할 수 있는 것을 알 수 있다. 사이클이 발생하는 경우 무조건 SCC에 해당한다는 특징이 있다. 그래서 위와 같이 방향 그래프일 때만 의미가 있다. 무향 그래프라면 그 그래프 전체는 무조건 SCC이기 때문이다.
SCC를 추출하는 대표적인 알고리즘은 코사라주 알고리즘(Kosaraju's Algorithm)과 타잔 알고리즘(Tarjan's Algorithm)이 있다. 일반적으로 코사라주 알고리즘이 더 구현이 쉽지만 타잔 알고리즘이 더 적용이 쉽다.
타잔 알고리즘은 모든 정점에 DFS를 수행하여 SCC를 찾는 알고리즘이다. 부모로 돌아올 수 있어야 SCC가 성립될 수 있다. 구체적으로 이것을 검증하기 위해 부모에게 자식으로 나아가는 알고리즘으로 DFS 알고리즘이 사용되는 것이다.
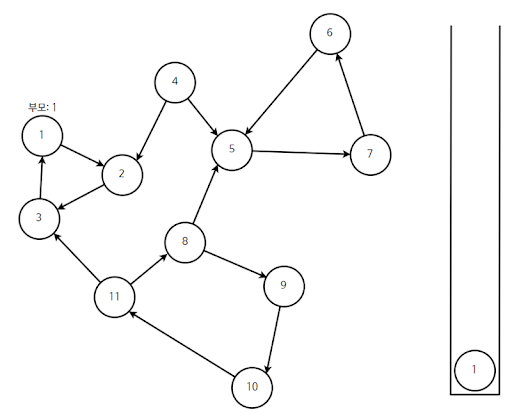
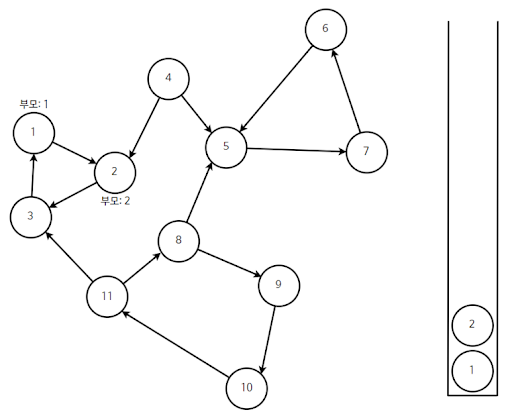
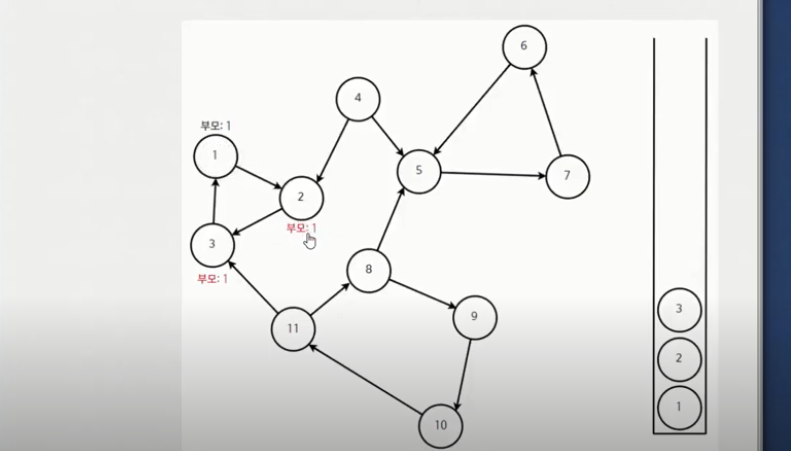
정점 3을 기준으로 DFS를 수행할 때 연결된 정점 1을 확인한다. 이 때 정점 1의 DFS가 끝나지 않은 상태이므로 여기에서 정점 3은 '아, 나의 부모가 정점1이구나'하고 파악한다.
이렇게 정점 3에 대한 DFS 함수가 끝나고, 정점 2의 부모 값은 정점 3에서 건너온 부모 값 1로 갱신됩니다. 따라서 정점 2의 부모 값도 1이 되었습니다.
그 다음, 정점 2에 대한 DFS 함수가 끝나고 정점 1의 부모 값은 정점 2에서 건너온 부모 값 1과 비교해서 동일하게 1이므로 유지됩니다. 이후에 함수가 마치면서 1의 부모 값은 자기 자신과 동일하기 때문에 '아 내가 SCC의 부모에 해당하는 것이었구나' 파악한 뒤에 스택에서 자기 자신이 나올 때까지 뽑습니다.
결과적으로 정점 1, 정점 2, 정점 3이 스택에서 나오고 하나의 SCC 그룹을 발견하게 되었습니다.
#include <iostream>
#include <vector>
#include <stack>
#define MAX 10001
using namespace std;
int id, d[MAX];
bool finished[MAX];
vector<int> a[MAX];
vector<vector<int>> SCC;
stack<int> s;
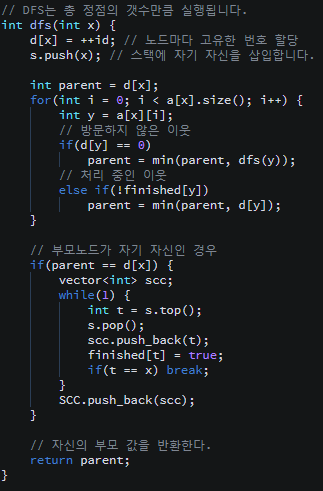
// DFS는 총 정점의 갯수만큼 실행됩니다.
int dfs(int x) {
d[x] = ++id; // 노드마다 고유한 번호 할당
s.push(x); // 스택에 자기 자신을 삽입합니다.
int parent = d[x];
for(int i = 0; i < a[x].size(); i++) {
int y = a[x][i];
// 방문하지 않은 이웃
if(d[y] == 0)
parent = min(parent, dfs(y));
// 처리 중인 이웃
else if(!finished[y])
parent = min(parent, d[y]);
}
// 부모노드가 자기 자신인 경우
if(parent == d[x]) {
vector<int> scc;
while(1) {
int t = s.top();
s.pop();
scc.push_back(t);
finished[t] = true;
if(t == x) break;
}
SCC.push_back(scc);
}
// 자신의 부모 값을 반환한다.
return parent;
}
int main(void) {
int v = 11;
a[1].push_back(2);
a[2].push_back(3);
a[3].push_back(1);
a[4].push_back(2);
a[4].push_back(5);
a[5].push_back(7);
a[6].push_back(5);
a[7].push_back(6);
a[8].push_back(5);
a[8].push_back(9);
a[9].push_back(10);
a[10].push_back(11);
a[11].push_back(3);
a[11].push_back(8);
for(int i = 1; i <= v; i++) {
if(d[i] == 0) dfs(i);
}
cout << "SCC의 갯수 : " << SCC.size() << endl;
for(int i = 0; i < SCC.size(); i++) {
cout << i + 1 << "번째 SCC : ";
for(int j = 0; j < SCC[i].size(); j++) {
cout << SCC[i][j] << " ";
}
cout << endl;
}
return 0;
}
강한 결합 요소(SCC)는 그 자체로는 큰 의미가 없고, 위상 정렬과 함께 생각해보았을 때 큰 의미가 있다. 모든 SCC를 각 정점으로 고려했을 때 각 SCC를 위상 정렬할 수 있다.
즉, 현재 SCC가 총 4개인데 이러한 SCC들을 기준으로 하여 위상정렬을 수행할 수 있다는 것이다. 또한 타잔 알고리즘의 시간 복잡도는 O(V + E)로 위상 정렬의 시간 복잡도와도 동일하다.
'Algorithm > Algorithm' 카테고리의 다른 글
| 이분 매칭(Bipartite Matching) (0) | 2020.07.26 |
|---|---|
| 네트워크 플로우(Network Flow) (0) | 2020.07.26 |
| 위상 정렬 알고리즘(Topology Sort) (0) | 2020.07.25 |
| 플로이드 와샬 알고리즘(Floyd Warshall Algorithm) (0) | 2020.07.25 |
| 다익스트라 알고리즘(Dijkstra Algorithm) (0) | 2020.07.25 |
- Total
- Today
- Yesterday
- 회전리스트
- call by reference
- call by value
- timecomplexity
- 직접 지정
- Algorithm
- 파이썬
- 구조체
- 형승격
- 공부
- 자료구조
- 비트필드
- 시간복잡도
- 프로그래밍
- 알고리즘
- 강의
- inflearn
- 배열
- 1차원 배열
- 공용체
- 재귀함수
- codeit
- 포인터
- 종류
- 2차원 배열
- 간접 지정
- 3차원 배열
- 다차원 배열
- C
- 공간복잡도
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |