티스토리 뷰
라빈 카프(Rabin-Karp) 알고리즘은 특이한 문자열 매칭 알고리즘입니다. 항상 빠르지는 않지만 일반적인 경우 빠르게 작동하는 간단한 구조의 문자열 매칭 알고리즘입니다. 라빈 카프 알고리즘은 해시(Hash) 기법을 사용합니다.
◆ abacaaba의 해시 값
= 97 * 2^7 +
98 * 2^6 +
97 * 2^5 +
99 * 2^4 +
97 * 2^3 +
97 * 2^2 +
98 * 2^1 +
97 * 2^0 +
= 24,834
물론 해시 값이 중복되는 경우도 발생할 수 있습니다. 이것을 충돌(Collision)이라고 하는데, 보통 발생률이 높지 않기 때문에 무시하고 넘아가는 것입니다. 실제로는 충돌이 발생하는 경우 포인터(Pointer)를 이용해 연결 자료구조를 이용해 해결합니다.(해쉬 체이닝 기법 등)
즉 라빈 카프 알고리즘은 '긴 글'과 '부분 문자열'의 해시 값이 일치하는 경우에만 문자여을 재검사하여 정확히 일치하는지 확인하는 알고리즘입니다.
라빈 카프 알고리즘은 문자열의 해시 값을 비교하여 그 일치 여부를 검사하는 알고리즘입니다.

그렇다면 위와 같이 한 칸 이동한 결과는 어떻게 빠르게 구할 수 있을지 알아봅시다. 바로 가장 앞에 있는 문자
'a'만큼의 수치를 빼 준 뒤에 2를 곱하고 새롭게 뒤에 들어온 'a'의 수치를 더해줍니다.
긴 글 해시 값 2 * (긴 글 해시 값 - 가장 앞에 있는 문자의 수치) + 새롭게 들어온 문자의 수치
위와 같은 공식을 사용하면 앞에서부터 뒤로 쭉 읽으면서 값을 구할 수 있어서 매우 빠른 것입니다.
#include <iostream>
using namespace std;
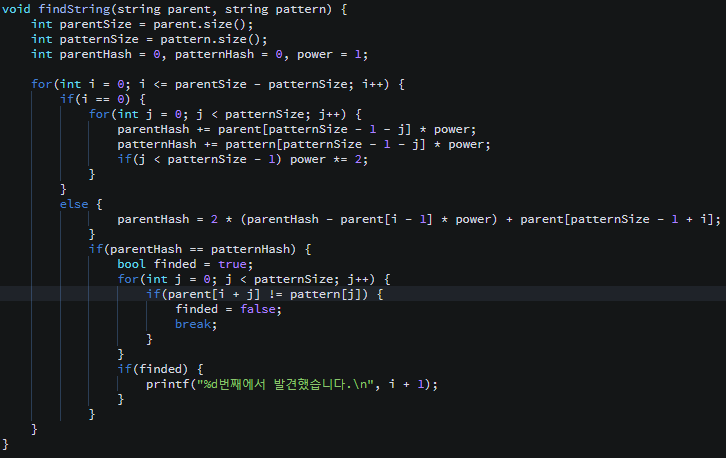
void findString(string parent, string pattern) {
int parentSize = parent.size();
int patternSize = pattern.size();
int parentHash = 0, patternHash = 0, power = 1;
for(int i = 0; i <= parentSize - patternSize; i++) {
if(i == 0) {
for(int j = 0; j < patternSize; j++) {
parentHash += parent[patternSize - 1 - j] * power;
patternHash += pattern[patternSize - 1 - j] * power;
if(j < patternSize - 1) power *= 2;
}
}
else {
parentHash = 2 * (parentHash - parent[i - 1] * power) + parent[patternSize - 1 + i];
}
if(parentHash == patternHash) {
bool finded = true;
for(int j = 0; j < patternSize; j++) {
if(parent[i + j] != pattern[j]) {
finded = false;
break;
}
}
if(finded) {
printf("%d번째에서 발견했습니다.\n", i + 1);
}
}
}
}
int main() {
string parent = "ababacabacaabacaaba";
string pattern = "abacaaba";
findString(parent, pattern);
return 0;
}
또한 정확하게 해시 값의 일치 여부를 검증하기 위해서 나머지(MOD)를 사용하는 경우가 많습니다. 하지만 일반적으로 오버 플로우(Over Flow)가 발생해도 해시 값 자체는 동일하기 때문에 나머지 연산을 굳이 사용해주지 않아도 되긴 합니다. 하지만 더 안정적인 프로그램을 작성하고자 하실 때는 나머지 연산(MOD)를 입혀주시는 것을 추천합니다.
'Algorithm > Algorithm' 카테고리의 다른 글
| KMP(Knuth-Morris-Pratt) 알고리즘 (0) | 2020.07.26 |
|---|---|
| 이분 매칭(Bipartite Matching) (0) | 2020.07.26 |
| 네트워크 플로우(Network Flow) (0) | 2020.07.26 |
| 강한 결합 요소 (Strongly Connected Component) (0) | 2020.07.25 |
| 위상 정렬 알고리즘(Topology Sort) (0) | 2020.07.25 |
- Total
- Today
- Yesterday
- C
- 1차원 배열
- 포인터
- call by reference
- 시간복잡도
- inflearn
- 파이썬
- 3차원 배열
- 공용체
- codeit
- 형승격
- 자료구조
- 공부
- 재귀함수
- 직접 지정
- 강의
- 2차원 배열
- call by value
- 구조체
- 다차원 배열
- 배열
- timecomplexity
- 회전리스트
- 종류
- 프로그래밍
- Algorithm
- 공간복잡도
- 알고리즘
- 비트필드
- 간접 지정
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |