티스토리 뷰
codeit 강의를 통해 배운,
알고리즘 성능에 대한 분석법을 소개하겠습니다.
알고리즘 성능 분석에는
1. 시간 복잡도 - Time complexity
2. 공간 복잡도 - Space complexity
지금 할 것은
시간 복잡도(Time complexity)란?
기본적으로, Big-O Notation 이라는 표기법을 사용합니다.
Big-O
- 시간 복잡도에 가장 큰 영향을 미치는 차항으로 시간복잡도를 나타내는 것을 Big-O 표기법 (Big-O Notation)
- 시간 복잡도의 표현 법 중 가장 많이 쓰이는 표현 법으로 알고리즘 실행 시간의 상한을 나타낸 표기법입니다. (최악의 효율)
T(n)=n^2+2n+9 # O(n^2)
T(n)=n^4+n^3+n^2+1 # O(n^4)
T(n)=5n^3+3n^2+2n+1 # O(n^3)Big-O 표기법의 종류와 성능
- O(1)
- O(logn)
- O(n)
- O(nlogn)
- O(n^2)
- O(n^3)
- O(n^4)
- O(2^n)
- O(n!)
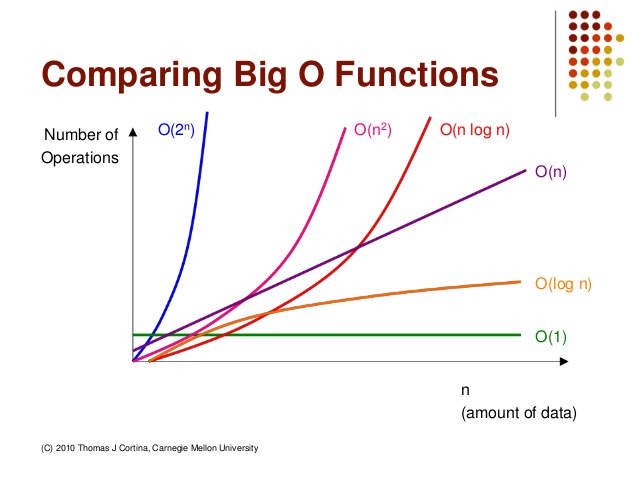
여기서 몇 가지의 예제를 통해 살펴보자면,
O(n^2)
# O(n^2) 함수
def print_pairs(my_list):
for i in range(len(my_list)):
for j in range(len(my_list)):
print(my_list[i], my_list[j])두 반복이 모두 input의 크기에 비례한다면 n*n이므로 O(n^2) 으로 볼 수 있습니다.
O(log n)
# O(lg n) 함수
# 2의 거듭제곱을 출력하는 함수
# (이번에는 인풋이 리스트가 아니라 그냥 정수입니다)
def print_powers_of_two(n):
i = 1
while i < n:
print(i)
i = i * 2반복문은 i가 2배씩 계속 늘어나므로 O(log n)으로 볼 수 있습니다.
# O(lg n) 함수
# 2의 거듭제곱을 출력하는 함수
# (이번에는 인풋이 리스트가 아니라 그냥 정수입니다)
def print_powers_of_two(n):
i = n
while i > 1:
print(i)
i = i / 2i를 1부터 시작해서 두 배씩 곱하는 게 아니라, n부터 시작해서 반씩 나눠봅시다.
이 경우에도 i가 128일 때부터 64, 32, 16, 8, 4, 2까지 반복문이 7번 실행됩니다.
O(nlog n)
def print_powers_of_two_repeatedly(n):
for i in range(n): # 반복횟수: n에 비례
j = 1
while j < n: # 반복횟수: lg n에 비례
print(i, j)
j = j * 2O(nlog n)은 O(n)과 O(log n)이 서로 합쳐진 형태입니다.
def print_powers_of_two_repeatedly(n):
i = 1
while i < n: # 반복횟수: lg n에 비례
for j in range(n): # 반복횟수: n에 비례
print(i, j)
i = i * 2이 경우도 O(nlog n) 입니다.
실습
a=5 # Constant 1
b=6 # Constant 1
c=10 # Constant 1
for i in range(n):
for j in range(n):
x = i * i # n^2 => for문 중첩 사용
y = j * j # n^2
z = i * j # n^2
for k in range(n):
w = a*k + 45 # n
v = b*b # n
d = 33 # Constant 1- T(n) = 3 + 3n^2 + 2n + 1 = 3n^2 + 2n + 4
- 이 경우에는 가장 큰 지수를 가진 n만을 생각하면 됩니다.
- O(n^2) 입니다.
'Algorithm > Algorithm' 카테고리의 다른 글
| ★ Union-Find 합집합 찾기 (0) | 2020.07.19 |
|---|---|
| C++ / 힙 정렬(Heap Sort) (0) | 2020.07.15 |
| [codeit] 재귀 함수 (Recursive Function) (0) | 2019.06.15 |
| 리스트 회전에 대한 알고리즘 (0) | 2019.06.11 |
| [codeit] Algorithm 공간 복잡도 (Space complexity) (0) | 2019.06.07 |
공지사항
최근에 올라온 글
최근에 달린 댓글
- Total
- Today
- Yesterday
링크
TAG
- 간접 지정
- 구조체
- 2차원 배열
- 공간복잡도
- 종류
- 자료구조
- C
- 형승격
- 시간복잡도
- 직접 지정
- 공용체
- 회전리스트
- 다차원 배열
- call by reference
- 알고리즘
- 비트필드
- 재귀함수
- inflearn
- Algorithm
- 1차원 배열
- 포인터
- 강의
- codeit
- timecomplexity
- 배열
- 프로그래밍
- 공부
- call by value
- 파이썬
- 3차원 배열
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
글 보관함